LeetCode 1766. Tree of Coprimes

DFS

There is a tree (i.e., a connected, undirected graph that has no cycles) consisting of n nodes numbered from 0 to n - 1 and exactly n - 1 edges. Each node has a value associated with it, and the root of the tree is node 0.

To represent this tree, you are given an integer array nums and a 2D array edges. Each nums[i] represents the ith node's value, and each edges[j] = [uj, vj] represents an edge between nodes uj and vj in the tree.

Two values x and y are coprime if gcd(x, y) == 1 where gcd(x, y) is the greatest common divisor of x and y.

An ancestor of a node i is any other node on the shortest path from node i to the root. A node is not considered an ancestor of itself.

Return an array ans of size n, where ans[i] is the closest ancestor to node i such that nums[i] and nums[ans[i]] are coprime, or -1 if there is no such ancestor.

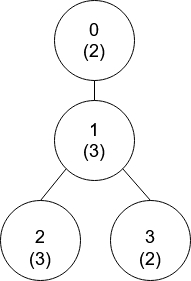
Example 1:

Input: nums = [2,3,3,2], edges = [[0,1],[1,2],[1,3]]
Output: [-1,0,0,1]
Explanation: In the above figure, each node's value is in parentheses.
- Node 0 has no coprime ancestors.
- Node 1 has only one ancestor, node 0. Their values are coprime (gcd(2,3) == 1).
- Node 2 has two ancestors, nodes 1 and 0. Node 1's value is not coprime (gcd(3,3) == 3), but node 0's
  value is (gcd(2,3) == 1), so node 0 is the closest valid ancestor.
- Node 3 has two ancestors, nodes 1 and 0. It is coprime with node 1 (gcd(3,2) == 1), so node 1 is its
  closest valid ancestor.

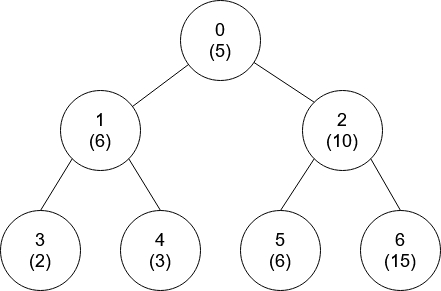
Example 2:

Input: nums = [5,6,10,2,3,6,15], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
Output: [-1,0,-1,0,0,0,-1]

Constraints:

• nums.length == n

• 1 <= nums[i] <= 50

• 1 <= n <= 105

• edges.length == n - 1

• edges[j].length == 2

• 0 <= uj, vj < n

• uj != vj

Solution:

English Version in Youtube

中文版解答Youtube Link

中文版解答Bilibili Link

class Solution {
    
    void dfs(int node, const vector<int>& nums, const vector<vector<int>>& graph,
             vector<int>& result,
             map<int, pair<int, int>>& ancestors /*value, {node, depth}*/,
             int depth, int parent) {
        int closest_ancestor = -1;
        int distance = INT_MAX;
        for (const auto& pair : ancestors) {
            if (__gcd(nums[node], pair.first) == 1 && (depth - pair.second.second) < distance) {
                distance = depth - pair.second.second;
                closest_ancestor = pair.second.first;
            }
        }
        result[node] = closest_ancestor;
        
        bool has_original_node = (ancestors.count(nums[node])) > 0;
        pair<int, int> original_node = ancestors[nums[node]];
        ancestors[nums[node]] = {node, depth};
        for (int neighbor : graph[node]) {
            if (neighbor == parent) {
                continue;
            }
            dfs(neighbor, nums, graph, result, ancestors, depth + 1, node);
        }
        ancestors.erase(nums[node]);
        if (has_original_node) {
            ancestors[nums[node]] = original_node;
        }
    }
    
public:
    vector<int> getCoprimes(vector<int>& nums, vector<vector<int>>& edges) {
        int n = nums.size();
        vector<vector<int>> graph(n);
        for (const vector<int>& edge : edges) {
            graph[edge[0]].push_back(edge[1]);
            graph[edge[1]].push_back(edge[0]);
        }
        
        map<int, pair<int, int>> ancestors;
        vector<int> result(n, -1);
        dfs(/*node=*/0, nums, graph, result, ancestors, /*depth=*/0, /*parent=*/-1);
        return result;
    }
};