LeetCode 1761. Minimum Degree of a Connected Trio in a Graph

You are given an undirected graph. You are given an integer n which is the number of nodes in the graph and an array edges, where each edges[i] = [ui, vi] indicates that there is an undirected edge between ui and vi.

A connected trio is a set of three nodes where there is an edge between every pair of them.

The degree of a connected trio is the number of edges where one endpoint is in the trio, and the other is not.

Return the minimum degree of a connected trio in the graph, or -1 if the graph has no connected trios.

Example 1: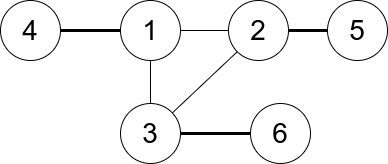

Input: n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]]
Output: 3
Explanation: There is exactly one trio, which is [1,2,3]. The edges that form its degree are bolded in the figure above.

Example 2: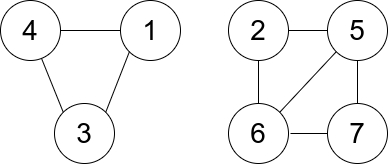

Input: n = 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]]
Output: 0
Explanation: There are exactly three trios:
1) [1,4,3] with degree 0.
2) [2,5,6] with degree 2.
3) [5,6,7] with degree 2.

Constraints:

• 2 <= n <= 400

• edges[i].length == 2

• 1 <= edges.length <= n * (n-1) / 2

• 1 <= ui, vi <= n

• ui != vi

• There are no repeated edges.

English Version in Youtube

中文版解答Youtube Link

中文版解答Bilibili Link

Solution1:

class Solution {
public:
    int minTrioDegree(int n, vector<vector<int>>& edges) {
        vector<unordered_set<int>> graph(n+1);
        
        for (const vector<int>& edge : edges) {
            graph[edge[0]].insert(edge[1]);
            graph[edge[1]].insert(edge[0]);
        }
        
        int ans = INT_MAX;
        for (int i = 1; i <= n; i++) {
            const unordered_set<int>& neighbors = graph[i];
            int tmp_a = graph[i].size() - 2;
            if (tmp_a >= ans) {
                continue;
            }
            for (int b : neighbors) {
                int tmp_b = tmp_a + graph[b].size() - 2;
                if (b < i || tmp_b >= ans) {
                    continue;
                }
                for (int c : graph[b]) {
                    if (neighbors.count(c) > 0) {
                        ans = min(ans, tmp_b + (int)graph[c].size() - 2);
                    }
                } 
            }
        }
        
        return ans == INT_MAX? -1 : ans;
    }
};

Solution2:

class Solution {
public:
    int minTrioDegree(int n, vector<vector<int>>& edges) {
        vector<vector<bool>> graph(n+1, vector<bool>(n+1, false));
        vector<int> degree(n+1, 0);
        
        for (const vector<int>& edge : edges) {
            graph[edge[0]][edge[1]] = true;
            graph[edge[1]][edge[0]] = true;
            degree[edge[0]]++;
            degree[edge[1]]++;
        }
        
        int ans = INT_MAX;
        for (int i = 1; i <= n; i++) {
            if (degree[i] < 2) continue;
            int tmp_a = degree[i] - 2;
            if (tmp_a >= ans) continue;
            for (int j = i + 1; j <= n; j++) {
                if (degree[j] < 2) continue;
                if (graph[i][j] == false) continue;
                int tmp_b = tmp_a + degree[j] - 2;
                if (tmp_b >= ans) continue;
                for (int k = j + 1; k <= n; k++) {
                    if (degree[k] < 2) continue;
                    if (graph[j][k] == false || graph[i][k] == false) {
                        continue;
                    }
                    ans = min(ans, tmp_b + degree[k] - 2);
                }
            }
        }
        
        return ans == INT_MAX? -1 : ans;
    }
};