Leetcode 1727. Largest Submatrix With Rearrangements

Greedy | Sort

You are given a binary matrix matrix of size m x n, and you are allowed to rearrange the columns of the matrix in any order.

Return the area of the largest submatrix within matrix where every element of the submatrix is 1 after reordering the columns optimally.

Example 1:

Input: matrix = [[0,0,1],[1,1,1],[1,0,1]]
Output: 4
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 4.

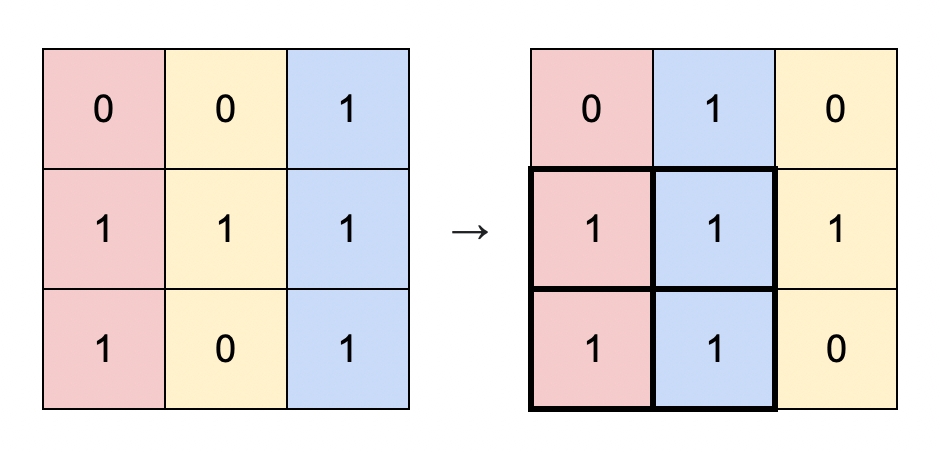
Example 2:

Input: matrix = [[1,0,1,0,1]]
Output: 3
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 3.

Example 3:

Input: matrix = [[1,1,0],[1,0,1]]
Output: 2
Explanation: Notice that you must rearrange entire columns, and there is no way to make a submatrix of 1s larger than an area of 2.

Example 4:

Input: matrix = [[0,0],[0,0]]
Output: 0
Explanation: As there are no 1s, no submatrix of 1s can be formed and the area is 0.

Constraints:

• m == matrix.length

• n == matrix[i].length

• 1 <= m * n <= 105

• matrix[i][j] is 0 or 1.

Solution:

English Version in Youtube

中文版解答Youtube Link

中文版解答Bilibili Link

• Transform the matrix, the value in each cell represents how many consecutive 1s below it.

• For each row, we can just sort in descending order; then iterate each column to find the maximal area.

class Solution {
public:
    int largestSubmatrix(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix.front().size();
        
        for (int j = 0; j < n; j++) {
            for (int i = m-1; i >= 0; i--) {
                if (matrix[i][j] == 1 && i != (m-1)) {
                    matrix[i][j] = 1 + matrix[i+1][j];
                }
            }
        }
        
        int ans = 0;
        
        for (int i = 0; i < m; i++) {
            sort(matrix[i].begin(), matrix[i].end(), std::greater<int>());
            
            for (int w = 0; w < matrix[i].size(); w++) {
                if (matrix[i][w] == 0) break;
                ans = max(ans, (w+1) * matrix[i][w]);
            }
        }
        
        return ans;
    }
};