LeetCode 1676. Lowest Common Ancestor of a Binary Tree IV

Tree

Given the root of a binary tree and an array of TreeNode objects nodes, return the lowest common ancestor (LCA) of all the nodes in nodes. All the nodes will exist in the tree, and all values of the tree's nodes are unique.

Extending the definition of LCA on Wikipedia: "The lowest common ancestor of n nodes p1, p2, ..., pn in a binary tree T is the lowest node that has every pias a descendant (where we allow a node to be a descendant of itself) for every valid i". A descendant of a node x is a node y that is on the path from node xto some leaf node.

Example 1: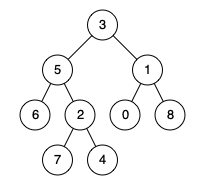

Input: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [4,7]
Output: 2
Explanation: The lowest common ancestor of nodes 4 and 7 is node 2.

Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [1]
Output: 1
Explanation: The lowest common ancestor of a single node is the node itself.

Example 3:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [7,6,2,4]
Output: 5
Explanation: The lowest common ancestor of the nodes 7, 6, 2, and 4 is node 5.

Example 4:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [0,1,2,3,4,5,6,7,8]
Output: 3
Explanation: The lowest common ancestor of all the nodes is the root node.

Constraints:

• The number of nodes in the tree is in the range [1, 104].

• -109 <= Node.val <= 109

• All Node.val are unique.

• All nodes[i] will exist in the tree.

• All nodes[i] are distinct.

Solution

English Version in Youtube

中文版解答Youtube Link

中文版解答Bilibili Link

class Solution {
    
    TreeNode* lowestCommonAncestor(TreeNode* root, const set<TreeNode*>& nodes_set) {
        if (root == nullptr) {
            return nullptr;
        }
    
        if (nodes_set.count(root) > 0) {
            return root;
        }
    
        TreeNode* l = lowestCommonAncestor(root->left, nodes_set);
        TreeNode* r = lowestCommonAncestor(root->right, nodes_set);
    
        if (l && r) {
            return root;
        }
    
        return l ? l : r;
    }
    
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, vector<TreeNode*> &nodes) {
        set<TreeNode*>nodes_set(nodes.begin(), nodes.end());
        return lowestCommonAncestor(root, nodes_set);
    }
};